Maim Chess was a 3^rd year Software Engineering (COMP 3653) project at Acadia University. The purpose of the project was to use the software engineering approaches covered in class to engineer, develop, and implement a program of my choice in its entirety from scratch. I chose a chess engine because of my interest in Artificial Intelligence. The entire time frame of the project was restricted to 8 weeks and 30 man hours, which was met. This time frame included the original and revised proposal, the engineering, designing, implementation and the 2,000 word final report of the project. Maim Chess was chosen as the name of the project as an incentive to create the strongest playing program possible within the time constraints.

Despite an obvious weakness in search depth due to the lack of transpositional tables (which could not be added due to time constraints), Maim Chess still plays at an estimated rating of about 2000 at 3 minutes / move (average time per move in tournament play) on a 200 MHz system. Playing at the standard 10 seconds / move, this rating would be approximately 150 points lower, given only 1/18^th the amount of thinking time (given twice the thinking time, a chess engine plays with a rating of approximately 50 to 70 ELO points higher against other computers, assuming optimizations such as transpositional tables exist, which Maim Chess does not have). This is good enough to demolish any beginner. To beat it, you will need to have a good understanding of positional play (probably better than the knowledge programmed into it), as the program is very unforgiving in tactical play. Given the fact that I understand all knowledge programmed into the game, since I have programmed everything I know about chess into it, the program plays at a disadvantage with me as I can often predict its moves.

Screen Shots:

Download: Maim Chess v0.31 (135KB)

The program should run on a 386+ processor.

Here is a game I played against Maim Chess set to think 10 seconds per move on a Pentium III 550 MHz processor. Although I made a tactical error, which Maim Chess capitalized on, I cramped its King and Bishop into the corner, rendering the Bishop useless, and its King in an awkward position. A cramped position like this is something that is relatively hard for computers to understand, even with deep analysis. Please view the game below using the MyChessViewer 2.2 Java PGN viewer, which I modified to use my own rendering (specifically for this applet) of the beautiful Chess Alpha font / piece set by Eric Bentzen.

Triple Jump is a checkers (draughts) playing program. It was a project created during my 3^rd year Artificial Intelligence course (COMP 3613) at Acadia University. The project was not required for the course, but the course raised my interest in Artificially Intelligent programs. So, I decided to implement one on my own. The project was completed in 2 weeks.

The name Triple Jump was chosen after the program was tested for the first time. This consisted of about 10 games against people on my floor. These games were played before any positional evaluation was programmed. The program was playing purely on tactics and no clue of where to place its checkers to higher its chances of winning - it was moving blindly. Only when human error introduced positions where it could benefit from tactical play within the scope of its search could it play anything meaningful. Needless to say, the program made short work of these opponents achieving a triple jump in every game, and finishing them off before even reaching the end game. It is very good at finding shots - where you give up pieces, but force a position to occur where you can gain back what you lost plus more. Once this happens, you will be down at least a piece, and should ultimately lose the game (with perfect play).

The program's main weakness is from lack of transpositional tables (repetition of a position in the search tree), and I will rewrite the program from scratch once I have time to implement this. The program suffers enormously from this for several different reasons. Notably, without these tables:

It also suffers from the lack of an end game database, and therefore plays the endgame poorly. Regardless, you have to be a very good checkers player to beat Triple Jump - you will only notice it's weak endgame play if you can reach the endgame. And even then, you cannot play carelessly - Triple Jump was once down 3 pieces to 4 against an experienced player, and it sacrificed a piece to set up a position in which it quadruple jumped all of the opponent's remaining pieces. Obviously embarrassed, the opponent left without saying a word - I would expect that this was probably the only game ever in which an experienced player suffered a quadruple jump to lose the game. This is just an indication that you cannot start to play carelessly at any point during a game, or you will probably lose.

Screen Shots of Amazing Wins:

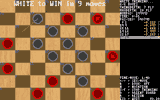
Some of the above pictures show amazing wins that Triple Jump solves. And you thought that checkers was a kids game... To announce a forced win, Triple Jump must analyze every possible outcome of the current position, all the way to the end of the game - where one side has either lost all his pieces, or rendered them immobile. For example, Triple Jump must see 17 moves ahead to announce a "White to Win in 9" - 9 moves for white, and 8 response moves for red.

In the first picture above, Triple Jump plays the most amazing win I have ever seen against an expert human player. Although Triple Jump is up by 2 pieces, and is going to win easily, it announces a White to Win in 8 moves in under a second in the position seen. Can you see the forced win? I could not see it until the very end of it's 8 move winning strategy. White sacrifices 6 pieces to force Red into a loss. The winning line of play is in the following table:

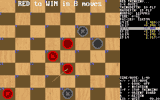
In the third picture above, Triple Jump solves an amazing position composed by D. Oldbury as a win for white in seconds. In case you are curious, best play for both sides is shown in the following table: Try it, and see!

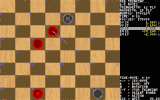
In the sixth picture above, Triple Jump is about to play 10-15, which appears to be an error! The move allows white's king to split the advancing pieces (by playing 7-10), something a complete beginner can see. White will win one of the two checkers in it's next move. Why would Triple Jump make such an error? It has not made an error - Triple Jump has just played a trap. Would you have fallen into it? If white falls for it by playing 7-10, red wins in five moves. Can you see the win? (Hint: first move to lead to win is 14-18 or 15-18)

Remember, the official rules for Checkers is that you must jump, if you can. This adds a lot of strategy to the game. It is, by no means, only a kids game.

I have a new found respect for checkers, now that I have played my computer program. The game is best described in this quote, from Marion Tinsley: "Playing chess is like looking out over a limitless ocean; playing checkers is like looking into a bottomless well." The quote is fairly accurate, as anyone can see that an ocean is limitless, however, it takes a greater amount of inspection to notice that a well is bottomless. Marion Tinsley was the World Checkers Champion for 45 years, losing only 5 games, of the thousands that he played, to only 3 individuals. This near perfection has been unmatched by any individual, in any other sport, ever. As quoted from the American Chess Journal, "To get an idea of the embarrassingly wide margin by which Tinsley surpasses his nearest competition, consider his defense of the world title in 1989 against the challenger Paul Davis. Tinsley drew 23 games, won 9, and lost 0."

Download: Triple Jump v0.30 (212KB)

The program should run on a 386+ processor. I know the user interface is not the greatest in this program, and I apologize for this.

Tic-Tac-Toe was a grade XII computer programming final project. The course taught Q-BASIC, and the second-to-last project covered double-nested loops! Considering that I used a FOR-NEXT loop in probably one of the first BASIC programs I had ever written in grade II, this was not a very challenging course, needless to say. The final project was a random question out of the final chapter of the book. Since my question was very simple, I asked to program an artificially intelligent tic-tac-toe program instead, and the teacher accepted.

The program is coded in BASIC, and does not use search tree methods. All AI is programmed via patterns in the board. There are 4 levels of difficulty, each level checks for more patterns (threats) and plays tougher. The highest level, as you probably guessed, will never lose.

Download: Tic-Tac-Toe (290KB)

Q-BASIC (included) is required to run the source code.